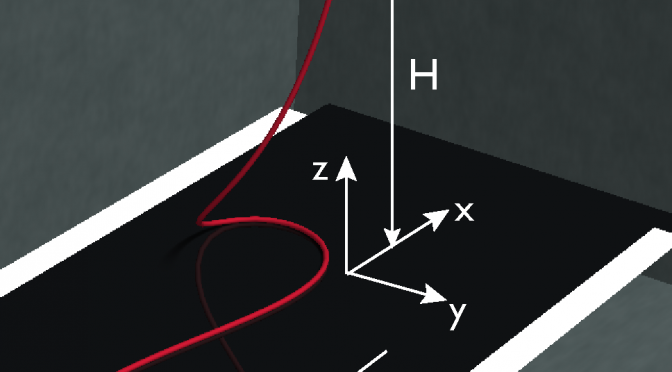
Submarine cables and fuel pipelines are typically deployed underwater from a cable-laying vessel. Operation PLUTO during World War II and the first transatlantic telegraph cable are two historical examples. Inspired by this, we consider a model desktop experiment where slender elastic rod is injected onto a moving conveyor belt. We explored this system, known as the elastic sewing machine, through a combination of precision desktop experiments and computer simulations
Experiments: We fabricated a meter-sized model setup, and injected elastomeric rod onto a conveyor belt. The injection speed and belt speed were carefully controlled. Sizing down the kilometer scale problem onto a desktop is possible owing to the scale-invariance of the mechanics of slender structures.
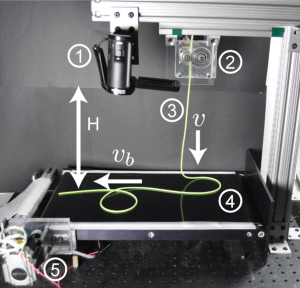
Figure: Photograph of the experimental apparatus. An injector (2) deploys an elastomeric rod (3) at a speed, v, from a height, H, onto the belt (4) moving at speed, vb, driven by a stepper motor (5). A video camera (1) records the process.
Numerical simulations: We employed the Discrete Elastic Rods (DER) tool for numerical simulation of the deployment process. DER was originally developed for simulation of hair, fur and other rod-like structures targeting the movie industry. The source code for simulations is here.
Pattern formation: Depending on the difference in speed between the injector and the belt, fascinating periodic patterns can form. For a visual abstract, click here.
When the belt is fixed, the rod coils in a circular fashion. We call it Static coiling. The figures below include experiments (green rod) and simulations (red rod) without any fitting parameter.
However, if the rod has natural curvature (typically induced from storing of cables spooled around a cylinder), it periodically changes the direction of coiling from clockwise to anticlockwise (or vice versa).
When the belt is moving, we see a variety of patterns. Some are shown below.
Towards a physical understanding: We observe four main patterns: meandering, alternating loops, translated coiling, and stretched coiling. In the figure below, we show the phase diagram along belt speed and injection speed, and find that the various regions are separated by straight lines passing through the origin. This indicates the pattern formation to be governed by the dimensionless speed mismatch, (v-vb)/v, which we take as the primary control parameter.
Click here for a standalone version of this plot.
We provide detailed analysis of the pattern formation process, and universal description of the pattern morphology, see our publications [PNAS 2014, EML 2014] for details.
Geometric model: When a thin thread of honey is poured onto a moving belt, patterns similar to the ones described above form. Click here for a video from U. Toronto. This system, known as the Fluid Mechanical Sewing Machine (FMSM), is similar to our Elastic Sewing Machine only in geometry. The constitutive description of honey (or viscous fluid) is very different from that of an elastic solid. It underlines the importance of geometry in both the processes, and encouraged us to form a Geometric Model (GM). The GM describes the pattern formation process from a geometric point of view, and allows for physical insight (details in this paper).
In the figure below, the regions of stability of various patterns along our control parameter, the dimensionless speed mismatch, in the Elastic Sewing Machine (ESM) and Fluid Mechanical Sewing Machine (FMSM) are shown. These regions are computed using both the Discrete Elastic Rods (DER), or Discrete Viscous Rods (DVR) in case of FMSM, and the Geometric Model (GM). The results for FMSM are obtained from Brun et al, 2015. It should be surprising to note the quantitative similarity in pattern formation in these two distinct systems.
Click here for a standalone version of the plot below.
Publications
- Jawed, M. K., Brun, P. T., Reis, P., “A geometric model for the coiling of an elastic rod deployed onto a moving substrate” Journal of Applied Mechanics 82:12, 121007 (2015)
- Jawed, M. K., Reis, P., “Pattern morphology in the elastic sewing machine” Extreme Mechanics Letters 1, 76-82 (2014)
Inaugural issue of Extreme Mechanics Letters - Jawed, M. K., Da, F., Jungseock, J., Grinspun, E., Reis, P., “Coiling of elastic rods on rigid substrates” Proceedings of the National Academy of Sciences 111:41, 14663-14668 (2014)
Press coverage: MIT News, Columbia Engineering,
Science Daily, Nanowerk, Phys.org
Coauthors
Pedro Reis (MIT), Fang Da (Columbia), Jungseock Joo (UCLA), Eitan Grinspun (Columbia), Pierre-Thomas Brun (MIT)